Least sqaure 개념과 설명

Least square (LS) 정리

1. Linear algebra

선형대수에 대한 기본적인 설명을 먼저하고 LS에 대해 소개한다.

아래와 같은 연립방정식이 있다고 하자. \[ \begin{aligned} 2x_1+x_2 = 2\\
x_1+2x_2 = 1 \end{aligned} \] 인 경우에, $x_1=1, x_2=0$로 해를 얻을 수 있다.

이걸 행렬로 표현하면 아래와 같이 표현이 된다. \[ \begin{aligned} A\mathbf{x} = \mathbf{b}, \text{where } A = \begin{bmatrix} 2 & 1 \\
1 & 2 \end{bmatrix}, \mathbf{x} = \begin{bmatrix} x_1 \\
x_2 \end{bmatrix}, \mathbf{b} = \begin{bmatrix} 2 \\
1 \end{bmatrix} \end{aligned} \]

역행렬을 취하면, \[ \mathbf{x} = A^{-1}\mathbf{b}= \begin{bmatrix} 1 \\
0
\end{bmatrix} \] 로 마찬가지로 해를 얻을 수 있다.

일반적으로 연립방정식은 변수와 등식의 개수가 동일하면, 해를 얻을 수 있다. (위의 예에서는, 두 개의 변수와 두 개의 등식)

만약에 아래처럼, 두 개의 변수가 있는데, 세 개의 등식이 있으면 어떻게 될까? \[ 2x_1+x_2 = 2\\
x_1+2x_2 = 1\\
x_1+3x_2 = 0 \] 이럴 경우, 근사 값 $\hat{\mathbf{x}}$를 찾아서 $A\hat{\mathbf{x}}$가 $\mathbf{b}$에 최대한 가깝도록 $\hat{\mathbf{x}}$를 찾아야 한다. 즉, $\min_{\mathbf{x}} ||A{\mathbf{x}}-\mathbf{b}||$를 찾아야 하고, 이러한 문제를 최소자승법, least-square method라고 한다.

2. Least square method

Least square가 의미하는 것은 error $||A{\mathbf{x}}-\mathbf{b}||^2_2$가 최소가 되도록 하는 것이고, 이를 풀어서 쓰면 아래와 같이 된다. \[ \begin{aligned} E &= (A\mathbf{x}-\mathbf{b})^T(A\mathbf{x}-\mathbf{b}) \\
&= \mathbf{x}^T A^T A \mathbf{x} - 2 \mathbf{b}^T A \mathbf{x} + \mathbf{b}^T \mathbf{b} \end{aligned} \]

$E$를 vector calculation을 통해 $\mathbf{x}$에 대해 미분하면,

\[ \frac{dE}{d\mathbf{x}}=2A^T A x - 2 A^T b \] 가 되어 $\frac{dE}{d\mathbf{x}}=0$인 $\mathbf{x}$는

\[ A^T A \mathbf{x} = A^T \mathbf{b} \] 를 만족한다.

만약 $A^T A$이 invertible하면,

\[ \mathbf{x} = (A^T A)^{-1} A^T \mathbf{b} \] 로 얻어진다.

3. Least Square의 기하학적 해석

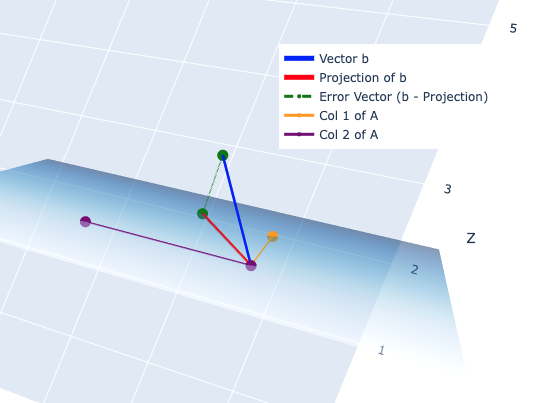
$A$의 column들로 이루어진 column space를 시각화하면, 아래 그림처럼 Col 1 of A $(a_1)$와 Col 2 of A $(a_2)$의 weighted sum인 평면으로 보여진다.

예를 들어서 위 세 개의 등식의 예인 경우, $a_1=[2, 1, 1]$과 $a_2=[1, 2, 3]$의 linear combination이 $A$의 column space다. $A\mathbf{x}$는 A의 column space에 머무르기 때문에, $||A{\mathbf{x}}-\mathbf{b}||$를 최소화 하는 $\mathbf{x}$는 $A$와 orthogonal하다.

즉, \[ A^T (A{\mathbf{x}}-\mathbf{b}) = 0 \] 을 만족해야한다.

이 식을 풀면 위 와 동일한

\[ A^T A \mathbf{x} = A^T \mathbf{b} \] 를 얻을 수 있다.

그러면, 한 단계 더 나아가서, $\hat{\mathbf{x}}=(A^T A)^{-1} A^T \mathbf{b}$로부터 $\mathbf{b}$를 A의 column space에 projection한 점인 $A\hat{\mathbf{x}}= A (A^T A)^{-1} A^T \mathbf{b}$임을 알 수 있고,

임의의 벡터를 A의 column space에 projection하는 matrix는 $A (A^T A)^{-1} A^T$라는 걸 알 수 있다.

4. $A^T A$이 Singula인 경우 (Invertible 하지 않은 경우)

여전히 \[ A^T A \mathbf{x} = A^T \mathbf{b} \] 를 만족하면 되지만, 최소로 만드는 $\mathbf{x}$는 유일하지 않다.

\[ \mathbf{x}_{LS} = A^+ \mathbf{b} + (I-A^+ A)y,\text{ where } y\in \mathbb{C}^n \] Null space

To be written …